1) Extensions of the Arimoto-Blahut Algorithm

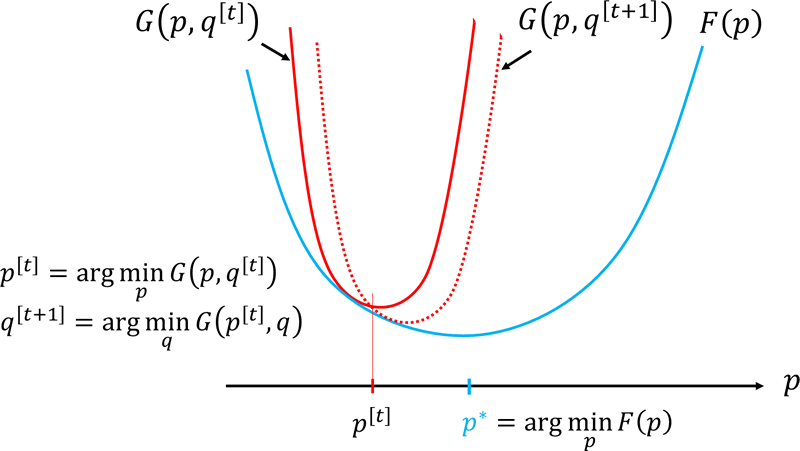
The bounds on various coding problems in information theory are often expressed in terms of solutions to optimization problems. The Arimoto-Brahat algorithm is an iterative algorithm that finds a probability distribution that achieves the channel capacity of a discrete memoryless channel and the rate-distortion function of a discrete memoryless source and is guaranteed to converge to an optimal value. Current information theory investigates the performance limits of many multi-user communication coding problems, often requiring computation algorithms. We study extensions of the Arimoto-Brahat algorithm to such problems.

2) Joint radar and communication using Gabor division multiplexing

Our laboratory studies Gabor-division multiplexing communications with the aim of realizing highly reliable information communications for high-speed moving vehicles, communications with Low Earth Orbit (LEO) satellites, and underwater acoustic communications that are subject to large Doppler frequency shifts. This is our group’s original method of simultaneous time and frequency division multiplexing, which can estimate and compensate for the Doppler shift.

3) Applied Researches in Deep Learning

Radiologists must be trained to read 3D MRI and CT images to determine the presence or absence of lesions. In the future, artificial intelligence is expected to be able to detect abnormalities in medical images with a high degree of confidence, surpassing the capabilities of expert radiologists. Our laboratory is investigating signal processing techniques for MRI and other medical images to help doctors make better diagnoses.

4) AD converters and random number generators based on chaotic dynamical systems

The study of (discrete) dynamical systems discusses the behavior and properties of the series x_n generated by the recurrence relation \(x_{n+1} = f ( x_n )\) given a function \(f\) from real to real and an initial value \(x_0\).
Using \(x_n4\) generated by the function \( B (x) = 2x\) (if \(0 \le x \le 1/2\) ), \(B(x) = 2x-1\) ( if \( 1/2 < x \le 1\) ) on the interval \(I = [0,1]\) and the threshold functions \(Q(x) = 0\) (if \( 0 \le x \le 1/2\)), \(Q(x) = 1\) ( if \(1/2 < x \le 1\) ), \(Q(x_n)\) is the \(n\)-th bit of the binary expansion of the initial value \(x_0\).
This is why \(B(x)\) is called a binary expansion map (or Bernoulli map). The random selection of the initial value \(x_0\) according to a uniform distribution over the interval I corresponds to a stochastic process in which \(0\) and \(1\) occur with probability \(1/2\).
In our laboratory, we study the properties of AD converters using the \(\beta\)-transformation \(f_{\beta, \theta}(x) = \beta x\) (if \( 0 \le x \le \theta\) ) and \(B(x) = \beta x-1\) (if \(\theta < x \le 1\) ), where \(\theta\) is a threshold, and its application as a random number generator.